Модель поверхностного дефекта конечной длины при нормальном намагничивании переменным магнитным полем и расчет топографии его магнитостатического поля.
Предложена расчетная модель магнитного поля поверхностного дефекта прямоугольного сечения конечной длины при нормальном намагничивании контролируемой поверхности. Получены удобные для практики выражения для вычисления фазового угла между мнимой и действительной составляющими. Предложен алгоритм оценки параметров дефекта и принципы построения устройств электромагнитной дефектоскопии и дефектометрии.
В работе [3] была предложена расчетная модель магнитного поля поверхностного дефекта прямоугольного сечения бесконечной протяженности при нормальном намагничивании контролируемой поверхности.
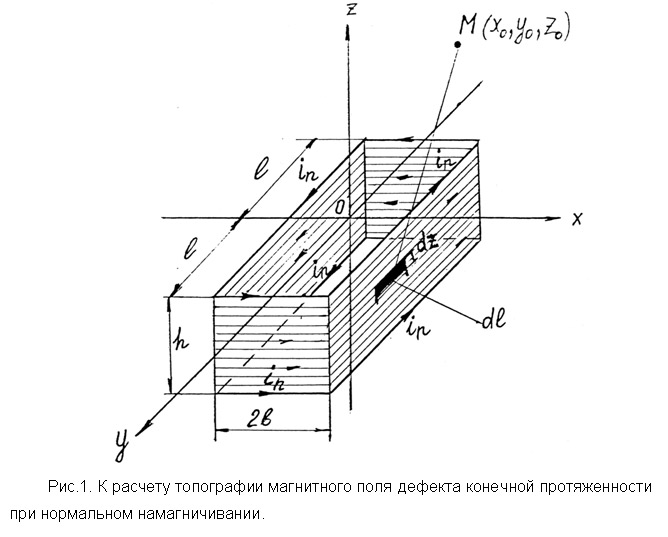
Рассмотрим влияние конечной протяженности дефекта 2l на величину магнитного поля поверхностного дефекта при нормальном намагничивании.
Рис.1. К расчету топографии магнитного поля дефекта конечной протяженности при нормальном намагничивании.
Расчетные и экспериментальные (по[2], рис.2) зависимости магнитного поля дефекта от частоты намагничивающего поля (нормальное намагничивание), ширина дефекта 2b= 0,5 мм, =300, = 3,3·106 См/м
| f,кГц | 16 | 32 | 40 | 48 | 64 | 80 | 96 | |
| 3,97 | 5,61 | 6,28 | 6,88 | 7,94 | 8,88 | 9,73 | ||
| h=1,7 мм | 0,045 | 0,064 | 0,071 | 0,078 | 0,09 | 0,1 | 0,11 | |
| h =3,0 мм | 0,079 | 0,112 | 0,126 | 0,138 | 0,16 | 0,178 | 0,196 | |
| H =5,0 мм | 0,132 | 0,187 | 0,209 | 0,229 | 0,267 | 0,296 | 0,327 | |
| h =11,0 мм | 0,291 | 0,411 | 0,46 | 0,5 | 0,587 | 0,65 | 0,72 | |
| h =1,7 мм | 0,022 | 0,03 | 0,033 | 0,036 | 0,041 | 0,045 | 0,049 | |
| h =3,0 мм | 0,037 | 0,05 | 0,056 | 0,06 | 0,068 | 0,075 | 0,08 | |
| h =5,0 мм | 0,058 | 0,078 | 0,085 | 0,091 | 0,102 | 0,11 | 0,118 | |
| h =11,0 мм | 0,109 | 0,137 | 0,147 | 0,154 | 0,167 | 0,175 | 0,182 | |
| h =1,7 мм | 0,98 | 0,968 | 0,964 | 0,959 | 0,955 | 0,945 | 0,945 | |
| h =3,0 мм | 0,96 | 0,94 | 0,938 | 0,931 | 0,92 | 0,912 | 0,9 | |
| h =5,0 мм | 0,93 | 0,91 | 0,897 | 0,888 | 0,87 | 0,856 | 0,84 | |
| h =11,0 мм | 0,85 | 0,804 | 0,786 | 0,769 | 0,735 | 0,712 | 0,623 | |
| h =1,7 мм | 4,5 | 6 | 7 | 7,7 | 9,5 | 10 | 11,0 | |
| h =3,0 мм | 7,8 | 10,9 | 12 | 13,2 | 15 | 17 | 18 | |
| h =5,0 мм | 12,6 | 17 | 19 | 21,1 | 23 | 26 | 28,5 | |
| h =11,0 мм | 24 | 34 | 37 | 40 | 45 | 48 | 48 | |
| h =1,7 мм | 4 | 7 | 8 | 8,5 | 10 | 12 | 13 | |
| h =3,0 мм | 7 | 10 | 11 | 11 | 13 | 16 | 18 | |
| h =5,0 мм | 11 | 16 | 18 | 22 | 24 | 27 | 30 | |
| h =11,0 мм | 20 | 29 | 33 | 38 | 42 | 44 | 48 | |
| h =1,7 мм | 11,5 | 14,2 | 12,5 | 14 | 5 | 15 | 15 | |
| h =3,0 мм | 11,4 | 2 | 9 | 11 | 15 | 6,7 | 0,5 | |
| h =5,0 мм | 11,5 | 6 | 5,0 | 4,5 | 4,2 | 4 | 5 | |
| h =11,0 мм | 11,0 | 20 | 11 | 3,8 | 4,2 | 4,4 | — |
Таким образом, выражение (8) является примером решения обратной задачи — нахождения глубины дефекта через измеренные величины максимальных значений полученных при двух фиксированных зазорах Z1, и Z2. реализация данной функции может быть осуществлена при одновременном измерении двумя первичными магниточувствительными преобразователями, установленными один над другим с фиксированным зазором [1]
Определение глубины дефекта с учетом его протяженности 2l следует проводить, используя следующее выражение (5):
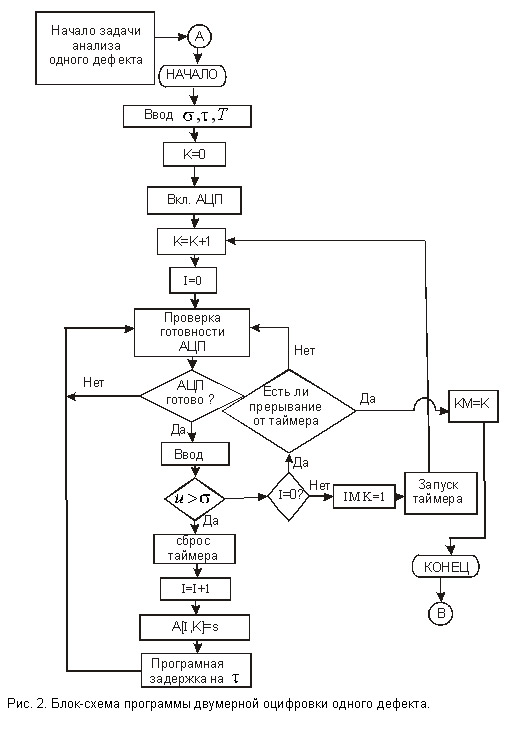
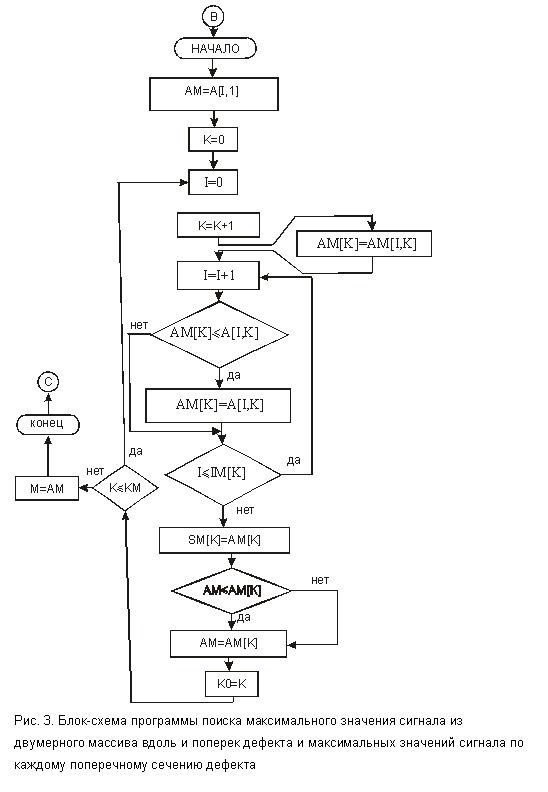
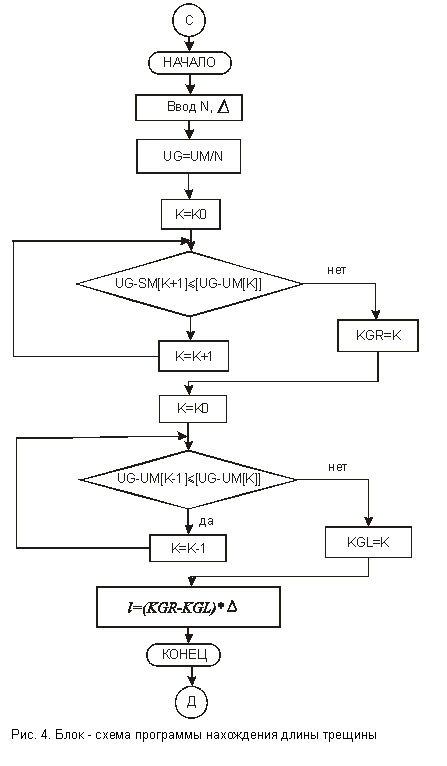
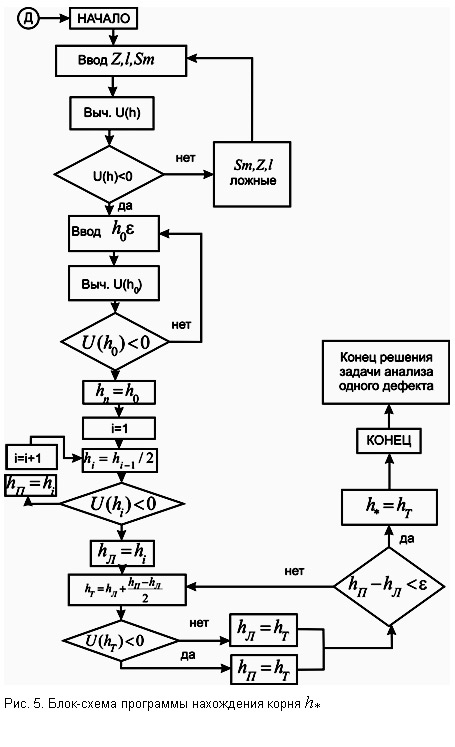
В этом случае вычисление h довольно трудоемкая задача, и возникает необходимость привлечения средств вычислительной техники. Для примера рассмотрим один из возможных алгоритмов оценки глубины дефекта с учетом его протяженности. На рис.2 — рис.5 приведены блок-схемы программ вычисления глубины h дефекта конечной протяженности 2l.
Вычисления осуществляются в такой последовательности. Предварительно производится двумерная оцифровка дефекта при сканировании первичного преобразователя поперек протяженности дефекта (рис.2). Здесь приняты следующие обозначения: U(t)— напряжение, пропорциональное магнитному полю, снимаемое с первичного преобразователя, -период опроса АЦП, T — период сканирования первичного преобразователя, — минимальный порог сигнала, равный напряжению на бездефектном месте, IM[k]- максимальное число точек над дефектом k-ом срезе (пересечении дефекта), КМ — число срезов на дефекте протяженностью l.
сканирование и обеспечивая не менее трех сечений над дефектом минимальной протяженности при заданном рабочем зазоре Z , сможем оценить глубину обнаруженного дефекта по отношению к минимально допустимому. Учитывая, что объектами контроля являются протяженные изделия проката, где, как правило, (более 90 %) имеются дефекты прокатного происхождения (типа волокон, трещин), недобраковки не будет. С целью повышения надежности контроля целесообразно устанавливать либо дифференциальные преобразователи проходного типа (если позволяет диаметр контролируемого изделия), либо дифференциальные накладного типа, установленные неподвижно.
Рассмотрим еще один способ оценки глубины дефектов, основанный на измерении фазового сдвига между действительной и мнимой составляющими магнитного поля. Сущность фазового метода раскрывается при анализе выражения (по [4], (20)), выведенного при изучении годографов вектора магнитного поля при нормальном намагничивании накладным индуктором. С учетом малости параметра A, проводя элементарные преобразования (разложение в ряд по аргументу) выражение (по [4], (20)), можно представить в таком виде
Как следует из (9) при малых значениях A фазовый угол пропорционален измеряемой глубине дефекта данный способ широко используется не только в практике электромагнитной дефектоскопии, но и в вихретоковой структуроскопии, благодаря высокой чувствительности, что позволяет применять одиночные первичные преобразователи магнитного поля (трансформаторные преобразователи).
ЛИТЕРАТУРА
- А.с. №1024819 (СССР). Способ электромагнитной дефектометрии./ Мужицкий В.Ф., Брон Ю.М., Лепешкин И.Н., Власов В.С., Болотный В.М. – опубл. в Б.И., 1983, № 23
- Зацепин Н.Н. Исследование магнитного поля вихревых токов над поверхностными дефектами. – Дефектоскопия, 1969, №4, с.104 – 112
- Мужицкий В.Ф. Модель поверхностного дефекта и расчет топографии его магнитного поля при нормальном намагничивании. – Дефектоскопия, 1988, №7, с.1 – 7
- Мужицкий В.Ф. Модель поверхностного дефекта и расчет топографии его магнитного поля при нормальном намагничивании переменным полем. Квазистационарный случай. – Дефектоскопия, 2004, №6, с.86 – 94