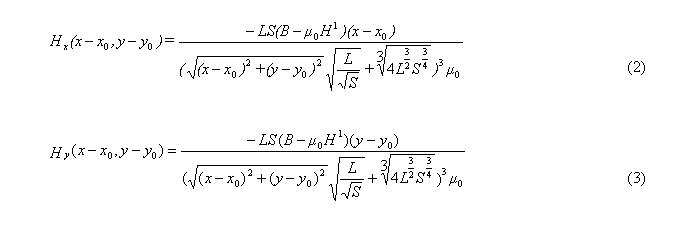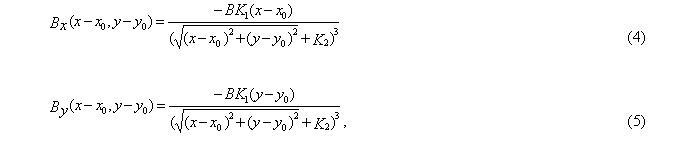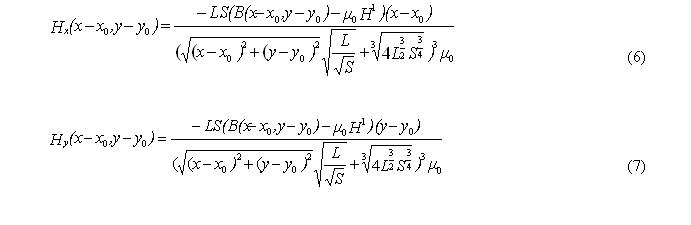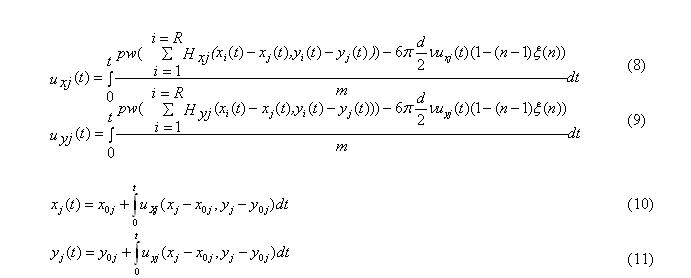ПОВЫШЕНИЕ ЧУВСТВИТЕЛЬНОСТИ МАГНИТОПОРОШКОВОГО МЕТОДА КОНТРОЛЯ.
Бакунов А.С., Кудрявцев Д.А., Ефимов А.Г., Онегин М. А. ЗАО «НИИИН МНПО «Спектр», Москва, Россия.

Доклад посвящен теме повышения чувствительности магнитопорошкового метода контроля путем определения параметров магнитной коагуляции, подходящих для выявления дефектов, и создания условий проведения магнитопорошкового контроля для получения данных параметров на практике.

Чувствительность магнитопорошкового метода определяется многими параметрами: напряженностью и характером намагничивающего поля, свойствами и размерами частиц магнитного порошка, вязкостью магнитной суспензии, свойствами поверхностно-активных добавок и др. При проведении магнитопорошкового контроля частицы магнитного порошка, попадая в магнитное поле, намагничиваются и притягиваются друг к другу, образуя цепочки, ориентированные по магнитным силовым линиям поля. Процесс образования цепочек из частиц порошка называют магнитной коагуляцией.

Выявляемость дефектов непосредственно связана с интенсивностью магнитной коагуляции. Интенсивная магнитная коагуляция делает индикаторные рисунки нечеткими, вызывает значительный фон из порошка, что значительно затрудняет расшифровку осаждений порошка. Кроме этого, осаждение порошка происходит не только над трещинами, но и над рисками, над местами грубой обработки поверхности. Короткие цепочки позволяют получить четкий рисунок над дефектами с большим градиентом поля (над усталостными, шлифовочными трещинами, волосовинами и др.). Они слабо осаждаются в полях малого градиента (над рисками, наклепом, карбидной полосчатостью и др.). Учитывая различную чувствительность цепочек к полям с различными значениями градиента поля можно, в зависимости от типа выявляемых дефектов, создать условия формирования цепочек частиц определенной длины, что позволит достигнуть высокой чувствительности к дефектам, подлежащим выявлению.

Расчет условий формирования цепочек частиц нужной длины затрудняет факт неоднородности поля над дефектом, под действием которого и происходит окончание процесса магнитной коагуляции и осаждение полученных цепочек частиц магнитного порошка над дефектом. В известных работах по магнитной коагуляции частиц магнитных суспензий (порошков) процесс формирования цепочек частиц в неоднородном магнитном поле дефекта не исследовался.
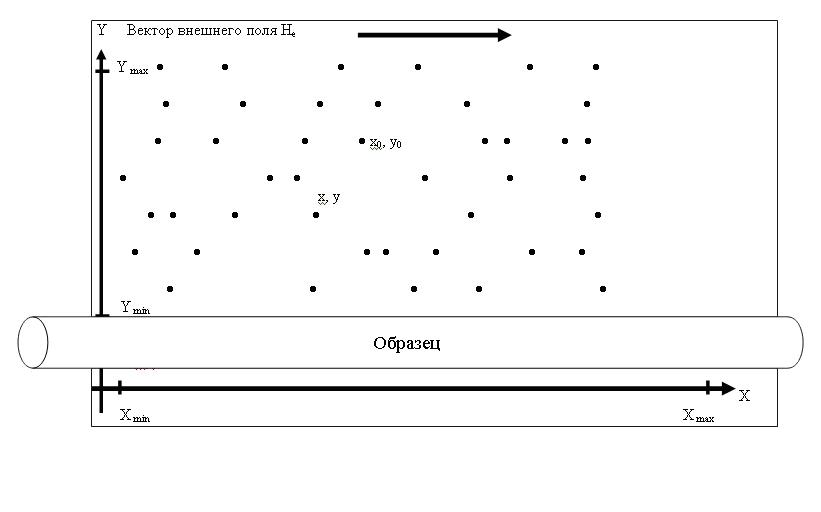
Рассмотрим процесс магнитной коагуляции частиц в неоднородном магнитном поле. Под действием внешнего постоянного магнитного поля дефекта He частицы намагничиваются до индукции B(He, L, S), (где L, S — соответственно, длина и площадь поперечного сечения частицы) и становятся магнитными диполями. На их противоположных торцевых поверхностях возникают магнитостатические заряды – магнитные полюсы N и S, ориентированные вдоль магнитных силовых линий внешнего поля He, как это показано на рис. 1.

Рис. 1. Распределение частиц магнитного порошка в плоскости над поверхностью образца.
Ymin, Ymax, Xmin, Xmax-координаты области случайного распределения частиц, х0 и у0 — координаты точки сосредоточения магнитного заряда частицы, х и у – координаты точки, где измеряется магнитное поле.

Вокруг частицы возникает магнитное поле, представляющее собой сумму полей магнитостатических зарядов намагниченных частиц H(х0, у0), и внешнего однородного постоянного магнитного поля He (рис. 1). Поскольку такие же поля возникают вокруг всех частиц, то на каждую j-тую частицу действует суммарное магнитное поле, в том числе и поле j-той частицы. Поле вокруг j-той частицы может быть определено по следующей формуле:
, (1)

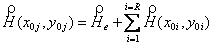
где R – число частиц.
В результате обработки данных измерений поля вокруг 23-х экспериментальных образцов и установления корреляционных связей между параметрами и результатами экспериментов были получены следующие выражения для составляющих вектора напряженности магнитного поля, создаваемого однородным постоянным магнитным полем вокруг намагниченной частицы или цепочки частиц:

где L – длина частицы (цепочки), отнесенная к длине вектора координат; S – площадь поперечного сечения частицы; B(x,y) – магнитная индукция; µо — магнитная проницаемость в вакууме; H1- напряженность намагничивающего магнитного поля; x, y – координаты точки измерения напряженности; xo, yo – координаты частицы (середины цепочки частиц).
Когда в пространство с однородным постоянным магнитным полем вводится образец с магнитными свойствами, то, в результате его намагничивания, в пространстве над образцом возникает неоднородное магнитное поле с магнитной индукцией B(x, y), величина которой зависит от координат в пространстве.
В результате установления корреляционных связей между параметрами и результатами экспериментов были получены следующие формулы составляющих вектора магнитной индукции этого неоднородного поля:

где К1 и К2 — коэффициенты, зависящие от магнитных свойств образца (К1 имеет значение в пределах от 4 до 5, а К2 — близок к единице).
Таким образом, после подстановки (4) и (5) в (2) и (3) формулы составляющих напряженности магнитного поля вокруг частицы будут иметь следующий вид:

Исходя из анализа сил, действующих на частицу порошка в магнитном поле (силы магнитного взаимодействия частиц и сила сопротивление движению частиц в суспензии), были выведены формулы составляющих скорости перемещения и координат j-той частицы (цепочки):

где ρ — магнитная восприимчивость частицы, w — объем частицы, d – диаметр частицы, ν – динамическая вязкость дисперсионной среды, ux и uy — составляющие вектора скорости движения частиц, n-число частиц в цепочке, ζ(n) –поправочный коэффициент на нелинейность формулы, m – масса частицы (цепочки), R – общее число частиц.
Критерий объединения частиц в цепочки: если расстояние между координатами x и y любых пар частиц (цепочек) становится меньше или равно диаметру сферы действия магнитных зарядов 2r, то частицы (цепочки) считаются объединившимися.
Полученные формулы координат частиц в текущий момент времени t позволяют произвести расчет параметров магнитной коагуляции по следующему алгоритму:
Задается случайное расположение R частиц, затем рассчитываются напряженности и силы взаимодействия всех R частиц, определяются их скорости и координаты. Проверяется расстояние между частицами, ищутся частицы, объединившиеся в цепочки. Все полученные данные заносятся в массив, затем определяются скорости и координаты частиц через период дискретизации Δt=0,01 с, вновь рассчитываются напряженности и силы взаимодействия всех частиц и проверяется расстояние между ними и т.д.
Задав размер частицы, концентрацию порошка в суспензии, вязкость суспензии, размеры дефектов, размеры области намагничивания и величину напряженности намагничивающего поля, можно получить зависимость длины получаемых в процессе магнитной коагуляции цепочек частиц от времени намагничивания и полива. Таким образом определяется время намагничивания tн, необходимое для образования цепочек с длиной, требуемой для качественного и надежного выявления дефектов заданных размеров.
Использование приведенного алгоритма позволяет создать условия проведения магнитопорошкового контроля, при которых в процессе магнитной коагуляции формируются цепочки частиц определенной длины с целью получения высокой чувствительности к дефектам, подлежащим выявлению.